遷移モーメント

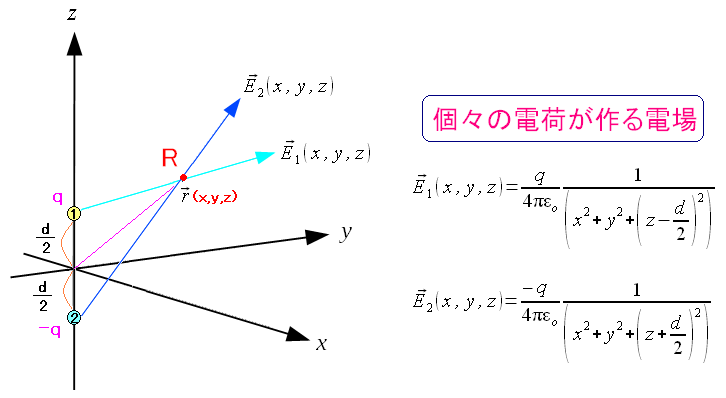
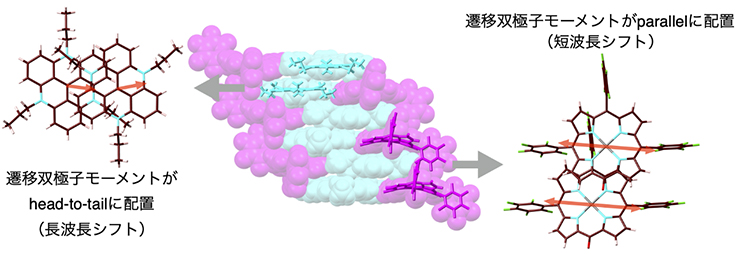
遷移モーメントとは、光（電磁波）による電子の遷移に関係する演算子のことである。

詳細

遷移確率

角振動数 ${\displaystyle \omega }$ で振動する相互作用${\displaystyle {\hat {H'}}}$が働いている量子系を考える場合，始状態${\displaystyle i}$から終状態${\displaystyle f}$への遷移確率は以下のように表される（フェルミの黄金率）．

${\displaystyle T_{i\rightarrow f}={\frac {2\pi }{\hbar }}\left|\langle f|{\hat {H'}}|i\rangle \right|^{2}\rho }$

ここで、${\displaystyle \rho }$ は 終状態の状態密度（単位エネルギーあたりの状態数）、${\displaystyle \langle f|{\hat {H'}}|i\rangle }$ は${\displaystyle {\hat {H'}}}$を行列表示した時の始状態と終状態についての行列要素であり，遷移モーメントと呼ばれる。

光と電子の相互作用

電磁場(光)の中の電子を考えた場合もフェルミの黄金率が適用でき，相互作用は以下で表される．

${\displaystyle {\hat {H}}'={\frac {e}{2m}}({\hat {\boldsymbol {p}}}\cdot {\hat {\boldsymbol {A}}} {\hat {\boldsymbol {A}}}\cdot {\hat {\boldsymbol {p}}} {\frac {e^{2}}{2m}}{\hat {A}}^{2})}$

ここで${\displaystyle {\hat {\boldsymbol {p}}}}$は電子の運動量，${\displaystyle {\hat {\boldsymbol {A}}}}$は電磁場のベクトルポテンシャルである．

光の波長に比べて電子系の大きさがずっと小さい場合、相互作用${\displaystyle {\hat {H'}}}$を電気双極子項${\displaystyle {\hat {\boldsymbol {P}}}}$、磁気双極子項${\displaystyle {\hat {\boldsymbol {L}}}}$、電気四極子項${\displaystyle {\hat {\Sigma x_{i}y_{i}}}}$などに分類することができる。

${\displaystyle {\hat {H}}'={\hat {\boldsymbol {P}}} {\hat {\boldsymbol {L}}} {\hat {\Sigma x_{i}y_{i}}} \dotsb }$

これらの遷移が起こるかどうかはそれぞれに対応する演算子${\displaystyle {\hat {\boldsymbol {P}}}}$、${\displaystyle {\hat {\boldsymbol {L}}}}$、${\displaystyle {\hat {\Sigma x_{i}y_{i}}}}$などの行列要素がゼロにならないかどうかで決まる。一般的には${\displaystyle {\hat {\boldsymbol {P}}}}$の行列要素が遷移確率に大きく寄与し，これが常にゼロになるような始状態と終状態の間の遷移は禁制遷移と呼ばれる．この場合は遷移確率が小さな値になるが，${\displaystyle {\hat {\boldsymbol {L}}}}$や${\displaystyle {\hat {\Sigma x_{i}y_{i}}}}$の行列要素がゼロでなければ，遷移は起こる．

参考文献

• 小出昭一郎 『量子力学(II) （改訂版）』 裳華房〈基礎物理学選書〉、1990年。ISBN 4-7853-2133-4。

関連項目

• 遷移双極子モーメント
• フェルミの黄金律