レナード-ジョーンズ・ポテンシャル

レナード-ジョーンズ・ポテンシャル（英: Lennard-Jones potential）とは、2つの原子間の相互作用ポテンシャルエネルギーを表す経験的なモデルの一つである。ポテンシャル曲線を表す式が簡単で扱いやすいので、分子動力学計算など、様々な分野において使われる。その名はレナード-ジョーンズにちなむ。

レナード-ジョーンズ・ポテンシャルは、実際のポテンシャル曲線を表現するための簡便な手法であり、少数のパラメータを用いたフィッティングに相当するため厳密ではない。しかし、問題の種類によっては、この方法で十分な場合がかなり多い。レナード-ジョーンズ・ポテンシャルに用いるパラメータは、実験的に求められた第二ビリアル係数、粘性係数、熱伝導率などから、推定することができる。他の原子間の相互作用のモデルポテンシャルとしては、モースポテンシャル(Morse potential)等が挙げられる。

レナード-ジョーンズ・ポテンシャルの数式による表記

レナード-ジョーンズ・ポテンシャル ${\displaystyle U(r)}$の一般形は、次の式であらわされる。

${\displaystyle U(r)=4\epsilon \left[\left({\frac {\sigma }{r}}\right)^{p}-\left({\frac {\sigma }{r}}\right)^{q}\right]}$　　(1)

ここで、${\displaystyle r}$は原子間距離(核間距離)である。${\displaystyle \sigma }$,${\displaystyle \epsilon }$は、フィッティングパラメータ（物理学的な意味は後述）で、これと、次数p,qを定めることによってレナード-ジョーンズ・ポテンシャルが一意に決まる。

特に引力項の次数q = 6、斥力項の次数p = 12とした

${\displaystyle U(r)=4\epsilon \left[\left({\frac {\sigma }{r}}\right)^{12}-\left({\frac {\sigma }{r}}\right)^{6}\right]}$　　(2)

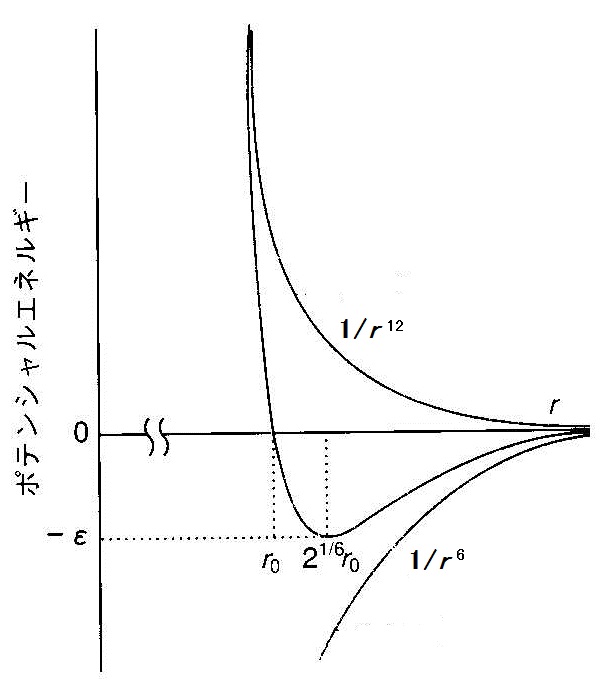
を、(6,12)ポテンシャルという。(6,12)ポテンシャルは、レナード-ジョーンズ・ポテンシャルの代表例である。以降、(6,12)ポテンシャルのことを、レナード-ジョーンズ・ポテンシャルとして説明する。${\displaystyle U(r)=Ar^{-12}-Br^{-6}}$のように簡単な形で書かれることもある。

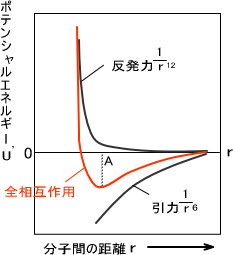
ここで、−6乗の引力項は、二つの原子の間の分散力、すなわち双極子-双極子間の相互作用によるものである。原子の永久双極子がゼロであっても、短時間をとった場合は電荷分布の揺らぎによる双極子が現れる。この双極子の電場により、もう一方の原子が分極し、誘起双極子が生じる。この相互作用ポテンシャルは原子間距離の-6乗に比例したものとなる。

一方、−12乗の斥力項は、電子雲の重なりによって反発力が働くためである。指数の−12は、−6乗のちょうど2乗で扱いやすいために選ばれることが多い。反発力の主な機構は、パウリの排他律によって、低いエネルギーの分子軌道に電子が入れないためである。

(1),(2)式より、${\displaystyle \sigma }$は距離の次元を持ち、${\displaystyle r=\sigma }$のときポテンシャルエネルギーがゼロになることがわかる。これより粒子間距離が小さい領域は−12乗の強い斥力に支配され、これ以上接近することが稀であることから、${\displaystyle \sigma }$を衝突直径と呼ぶことがある。また(1)式から、${\displaystyle \epsilon }$はエネルギーの次元を持ち、ポテンシャルの深さを表している。この2つのフィッティングパラメータ${\displaystyle \sigma }$,${\displaystyle \epsilon }$によって、レナード-ジョーンズ・ポテンシャルが一意に決まる。

これらのパラメータは粒子-粒子間の相互作用であるため、厳密には特定の物質が持つ物性ではない。理想的には全ての粒子種の組み合わせ（100を越える原子についてはおよそ5000組、ユナイテッドアトム・モデルまで拡張するとさらに増える）について、その全てが実験的事実から検討されることが望ましいが、現実的ではない。そのため、同種の粒子間力に関するパラメータを実験的に得て、ローレンツ-ベルテロ則を用いるなどして異種粒子間のパラメータを推算することが一般となっている。

ここで、原子の相対運動において角運動量がない（回転による遠心力がない）とした場合の、平衡原子間距離について考察する。(2)式を原子間距離${\displaystyle r}$で微分すると、原子間に働く力${\displaystyle F(r)}$が得られる(斥力を正とした)。

${\displaystyle F(r)=-{\frac {d}{dr}}U(r)=4\epsilon \left(12\,{\frac {{\sigma }^{12}}{r^{13}}}-6\,{\frac {{\sigma }^{6}}{r^{7}}}\right)}$　　(3)

(4)式で与えられる平衡原子間距離${\displaystyle r_{0}}$においては、${\displaystyle F(r_{0})=0}$となるため、(3)式を用いると以下の関係が成立する。

${\displaystyle r_{0}=2^{1/6}\sigma }$　　(4)

また、(2)式を${\displaystyle r}$で二階微分して、${\displaystyle r=r_{0}}$を代入すれば正値になるため、ポテンシャルエネルギーは${\displaystyle r_{0}}$において極小値をとり、安定点であることが確認できる。物質の格子定数は、この${\displaystyle r_{0}}$とよく一致する。

次に、${\displaystyle \epsilon }$が、ポテンシャルエネルギーの深さであることを示す。(2)式の${\displaystyle \sigma }$に(4)式を代入すると、次のようになる。

${\displaystyle U(r)=\epsilon \left[\left({\frac {r_{0}}{r}}\right)^{12}-2\left({\frac {r_{0}}{r}}\right)^{6}\right]}$　　(5)

したがって、2原子間の距離が${\displaystyle r=r_{0}}$のとき、(5)式は${\displaystyle U(r_{0})=-\epsilon }$となる。つまり、${\displaystyle r\rightarrow \infty }$の解離極限では、${\displaystyle U(r)\rightarrow 0}$であることを用い、零点振動を無視すれば、${\displaystyle \epsilon }$は2つの原子間の結合エネルギー（解離エネルギー）に相当することがわかる。

レナード-ジョーンズ・ポテンシャルの応用

レナード-ジョーンズ・ポテンシャルは計算化学およびソフトマター物理学において基礎的な重要性を持つだけではなく、現実の物質のモデル化においても重要である。 レナード-ジョーンズ・ポテンシャルは物質のふるまいの基礎的研究および原子にまつわる現象を解明するためによく使われる。 また、（我々が属する3次元空間ではなく）2次元あるいは4次元空間の物質の熱物理学的性質の研究といった特殊な問題に使われることもある。

レナード-ジョーンズ・ポテンシャルは分子モデル化にも広く使われている。 レナード-ジョーンズ・ポテンシャルは、基本的には2つの方法で分子モデル化に使われる：(1) 実在の物質の原子あるいは分子をレナード-ジョーンズ・ポテンシャルで直接モデル化する方法。これにより希ガスおよびメタンのように分散相互作用する球形粒子については非常に良い結果が得られる。メタンの場合には、水素原子が炭素原子に融合して全体として一分子となり、分子が球対称であると見なす。もっと複雑な分子をこのように単純化することもできるが、通常は結果が良くない。 (2) 実在の物質の分子を複数のレナード-ジョーンズ相互作用サイトで構成する方法。これらのレナード-ジョーンズ相互作用サイトは固いボンドによる接続または追加ポテンシャルによる柔軟な接続で繋がれている。この方法を使って、実質的に全ての分子およびイオン性粒子に対する（「力場」と呼ばれることもある）分子モデルを構成できる。

方法(1)で利用する場合、分子モデルで使えるパラメータはレナード-ジョーンズ・ポテンシャルのパラメータ ${\displaystyle \varepsilon }$ および ${\displaystyle \sigma }$ だけである。これらの値として例えばアルゴンでは ${\displaystyle \varepsilon /k_{\mathrm {B} }=120\,\mathrm {K} }$ および ${\displaystyle \sigma =0.34\,\mathrm {nm} }$ がよく使われる。 この方法が良い近似となるのは明らかに球状または単純な分散力で相互作用する原子または分子だけである。レナード-ジョーンズ・ポテンシャルを直接利用する方法(1)では、このポテンシャルに関する理論やシミュレーションの結果を直接利用できるという利点がある。 レナード-ジョーンズ・ポテンシャルに関して得られている結果を、適切な ${\displaystyle \varepsilon }$ および ${\displaystyle \sigma }$ （還元単位のセクション参照）を使うことでスケールして利用することができる。一般に、レナード-ジョーンズ・ポテンシャルのパラメータ ${\displaystyle \varepsilon }$ および ${\displaystyle \sigma }$ を実在の物質の任意の性質についてフィッティングで決定できる。ソフトマター物理では気液相平衡あるいは臨界点の実験データをパラメータ決定に使うことが多い。固体物理学では圧縮率、熱容量または格子定数を使うことが多い。

細長く複雑な分子の構成ブロックとしてレナード-ジョーンズ・ポテンシャルを使う方法(2)はもっとずっと洗練されている。 これにより、分子モデルはこの特定の分子についてだけ適用できるものになる。この分子力場の開発アプローチは今日ではソフトマター物理およびそれに関連する分野である化学工学、化学、および計算生物学で実施されている。たとえば TraPPE力場、OPLS力場、および MolMod力場 などの数多くの分子力場がレナード-ジョーンズ・ポテンシャルに基づいている。固体材料の最先端のモデリングでは、もっと精巧な多体ポテンシャル（たとえばEAMポテンシャル）を使う。

無次元還元単位

無次元還元単位はレナード-ジョーンズ・ポテンシャルのパラメータで定義できる。これらは分子シミュレーションで用いるのに便利である。数値計算の観点から見れば、 この単位系を使う利点として1に近い数を扱えること、方程式が単純になること、および結果をスケールすることが簡単になることがあげられる。この還元単位系では、レナード-ジョーンズ・ポテンシャルのサイズ・パラメータ ${\displaystyle \sigma }$ とエネルギー・パラメータ ${\displaystyle \varepsilon }$ および粒子の質量 ${\displaystyle m}$ を指定する必要がある。表に示したように、次元を考慮することで全ての物理量を単純に変換することができる。アスタリスクを使って還元単位系であることを示すことが多い。

一般に、長さパラメータおよびエネルギー・パラメータからなる他の分子相互作用についても、還元単位系を構成することができる。

レナード-ジョーンズ物質の熱物理学的性質

レナード-ジョーンズ物質、つまりレナード-ジョーンズ・ポテンシャルで相互作用する粒子系の熱物理学的性質は、統計力学を使って得ることができる。いくつかの性質は解析的に計算できるが、ほとんどの性質は分子シミュレーションを実行しなければ求めることができない。分子シミュレーションの結果には一般に、統計的不確実性と系統的不確実性の両方が含まれる。たとえばヴィリアル係数は代数的表式を用いて直接レナード-ジョーンズ・ポテンシャルから計算できるので、得られるデータに不確実性はない。それに対して、たとえば与えられた温度と密度における圧力に関する分子シミュレーションの結果は統計的および系統的不確実性を含んでいる。一般にレナード-ジョーンズ・ポテンシャルの分子シミュレーションは、分子動力学（molecular dynamics, MD）またはモンテ・カルロ（Monte Carlo, MC）シミュレーションである。MCシミュレーションではレナード-ジョーンズ・ポテンシャル ${\displaystyle V_{\mathrm {LJ} }(r)}$ をそのまま使うが、MDシミュレーションではポテンシャルの導関数、つまり力 ${\displaystyle {\boldsymbol {F}}=-{\boldsymbol {\nabla }}V_{\text{LJ}}(r)}$ を使う。この相違点に加えて、後述する長距離相互作用の扱いに関する違いが、熱物理的性質に関する結果に影響を与えることがある。

レナード-ジョーンズ粒子は単純だが現実的な粒子間相互作用のモデル化の典型例であるため、多数の熱物理学的性質が研究され、文献に報告されている。現在、レナード-ジョーンズ・ポテンシャルに関する計算機実験のデータは古典力学計算化学において最も正確に知られているデータであると考えられている。そのため、新しいアルゴリズムや理論の評価やテストのための比較対象として利用されることも多い。レナード-ジョーンズ・ポテンシャルは分子シミュレーションの初期の時代からずっと利用されてきた。1953年に「高速計算機械」上での分子シミュレーションが可能になったあとで、レナード-ジョーンズ・ポテンシャルに関する計算機実験の結果を最初に報告したのはローゼンブルースとローゼンブルース、およびウッドとパーカーであった。 それ以来、レナード-ジョーンズ物質のデータを報告する研究は多く、およそ50,000個のデータ点が公開されている。 レナード-ジョーンズ物質の熱物理学的性質に関する現状をまとめると、以下のようになる：シュテファンらが最も包括的なまとめとデジタルデータベースを与えている。現在は、このデータベースを完全に含み維持しているデータリポジトリはない。NIST websiteに示されている簡潔な選定データを扱う場合には、文献参照および選定範囲について注意すべきである。入手できるデータのごく一部しか含まれていないからである。NIST websiteに掲載されているデータの多くはNIST内の研究によるもので査読を受けていないデータである。

図2はレナード-ジョーンズ流体の相図である。レナード-ジョーンズ・ポテンシャルの相平衡はこれまでに何度も研究されており、そのため現在では精度よくわかっている。図2は計算機実験の結果から導かれた関係式の結果を示しているため、データ点ではなく線で表示している。

レナード-ジョーンズ粒子の一粒子あたりの平均粒子間相互作用は熱力学的状態、つまり温度と圧力（または密度）に強く依存する。固体状態、特に低温ではレナード-ジョーンズ相互作用の引力的部分が支配的となる。液体状態では固体状態に比べて秩序の低い構造を取る。一粒子あたりのポテンシャル・エネルギーは負になる。期待状態では、粒子間距離が大きいため、レナード-ジョーンズ・ポテンシャルの引力相互作用の影響は小さい。気体状態における内部エネルギーの大半は運動エネルギーである。超臨界状態でもレナード-ジョーンズ相互作用の引力部分の効果は小さい。温度を上げると粒子の平均運動エネルギーは増加し、レナード-ジョーンズ・ポテンシャルのエネルギー井戸の大きさを超える。すると粒子は主にソフト斥力で相互作用するようになり、その結果として平均ポテンシャル・エネルギーは正になる。

全体的に言えば、レナード-ジョーンズ・ポテンシャルとその熱物理学的性質の研究と文献発表の歴史が長く、精密なシミュレーションを実施する計算資源が（現代の標準から見て）不足していたため、かなりの量のデータが疑わしいことが知られている 。それにもかかわらず多くの研究でそのようなデータが参照されている。

特性点および曲線

レナード-ジョーンズ・ポテンシャルの最も重要な特性点は、臨界点および気体・液体・固体の三重点である。これらの点は文献で何度も研究されており、文献にまとめられている。 それらの研究により、臨界点は

${\displaystyle T_{\mathrm {c} }=1.321\pm 0.007\,\varepsilon k_{\mathrm {B} }^{-1}}$

${\displaystyle \rho _{\mathrm {c} }=0.316\pm 0.005\,\sigma ^{-3}}$

${\displaystyle p_{\mathrm {c} }=0.129\pm 0.005\,\varepsilon \sigma ^{-3}}$

にあると評価されている。

ここに与えた不確かさは、入手可能な気体・液体平衡に関する最も信頼できるデータセットから求めた臨界点パラメータの標準偏差から計算した。 現在は、三重点は

${\displaystyle T_{\mathrm {tr} }=0.69\pm 0.005\,\varepsilon k_{\mathrm {B} }^{-1}}$

${\displaystyle \rho _{\mathrm {tr,gas} }=0.0017\pm 0.004\,\sigma ^{-3}}$

${\displaystyle \rho _{\mathrm {tr,liq} }=0.845\pm 0.009\,\sigma ^{-3}}$

${\displaystyle \rho _{\mathrm {tr,sol} }=0.961\pm 0.007\,\sigma ^{-3}}$

${\displaystyle p_{\mathrm {tr} }=0.0012\pm 0.0007\,\varepsilon \sigma ^{-3}}$

にあると考えられている。これらの不確かさは、著者ごとにデータがばらついていることを表してる。レナード-ジョーンズ物質の臨界点は三重点よりずっと頻繁に研究されている。臨界点および気体・液体・固体三重点のどちらに関しても、上記の範囲外の結果を報告している研究がいくつかある。

明らかに、相共存線（図2参照）はレナード-ジョーンズ・ポテンシャルを特徴づけるのに重要な基礎的性質である。さらに、ブラウンの特性曲線により、レナード-ジョーンズ・ポテンシャルの本質的特徴を説明することができるようになる。ブラウンの特性曲線とは、いま対象としている物質のある熱力学量が、理想気体のそれと一致する曲線のことである。ギブズの相律の結果として、現実の流体では圧縮率因子${\displaystyle Z=p/\rho T}$とその導関数が理想気体の値と一致しうるのは、特定の${\displaystyle T}$と${\displaystyle \rho }$の組み合わせの場合だけである。結果として得られる点の集合は全体として特性曲線をなす。4本の主要な特性曲線が定義されている：そのうち0次曲線（つまり${\displaystyle Z}$が一致する曲線）は1本で、ゼノ曲線（Zeno curve）と呼ばれる。1次曲線（つまり${\displaystyle Z}$の一階導関数が一致する曲線）は3本ありアマガー曲線、ボイル曲線、およびシャルル曲線（Amagat, Boyle, and Charles curve）と呼ばれる。特性曲線は、両対数の圧力-温度平面上で負または0の曲率を持ち、一つの極大を持たなければならない。さらに、ブラウンの特性曲線とヴィリアル係数の間には理想気体極限で直接の関係があり、したがって${\displaystyle \rho \rightarrow 0}$の極限で特性曲線は厳密にわかる。レナード-ジョーンズ・ポテンシャルに関して、計算機シミュレーションの結果および状態方程式の結果のどちらも文献で報告されている。

図3にブラウンの特性曲線を示した。ゼノ曲線${\displaystyle \mathrm {Z} }$上の点では、圧縮率因子が1である：${\displaystyle Z=p/(\rho T)=1}$. ゼノ曲線はボイル温度${\displaystyle T_{\mathrm {B} }=3.417927982\,\varepsilon k_{\mathrm {B} }^{-1}}$から始まり、臨界点の周囲を周り、低温極限では傾き1を持つ。ボイル曲線${\displaystyle \mathrm {B} }$上の点では${\displaystyle \left.{\frac {\mathrm {d} Z}{\mathrm {d} (1/\rho )}}\right|_{T}=0}$である。ボイル曲線はボイル温度でゼノ曲線と共に始まり、臨界点の周囲を少し周りこんで、気体圧力曲線上で終わる。シャルル曲線（ジュール-トムソン逆転曲線とも呼ぶ）上の点は${\displaystyle \left.{\frac {\mathrm {d} Z}{\mathrm {d} T}}\right|_{p}=0}$かつ${\displaystyle \left.{\frac {\mathrm {d} T}{\mathrm {d} p}}\right|_{h}=0}$を持つ。つまり等エントロピー・スロットリングで温度が変化しない。シャルル曲線は理想気体極限で${\displaystyle T=6.430798418\,\varepsilon k_{\mathrm {B} }^{-1}}$から始まり、ゼノ曲線と交差し、気体圧力曲線上で終わる。アマガー曲線${\displaystyle \mathrm {A} }$上の点は${\displaystyle \left.{\frac {\mathrm {d} Z}{\mathrm {d} T}}\right|_{\rho }=0}$を持ち、理想気体極限で${\displaystyle T=25.15242837\,\varepsilon k_{\mathrm {B} }^{-1}}$から始まり、臨界点と他の3つの特性曲線を周りこんで固相領域に入り込む。レナード-ジョーンズ・ポテンシャルの特性曲線に関する包括的な議論は文献にある。

レナード-ジョーンズ流体の性質

ソフトマター物理およびそれに関連する分野でレナード-ジョーンズ・ポテンシャルは特に重要であるため、レナード-ジョーンズ流体の性質は文献で広く研究されている。2019年現在までに約50個の気液平衡に関する計算機実験結果のデータセットが公開されている。さらに、長年にわたって公開され続けている一様流体状態における35,000個以上のデータ点のまとめと外れ値の評価が、オープンアクセスデータベースにある。

レナード-ジョーンズ物質の気液平衡における蒸気圧、飽和密度、および界面張力を図4に示した。蒸気圧について±1%、飽和液体密度について±0.2%、飽和蒸気密度について±1%、気化エンタルピーについて±0.75%、そして表面張力について±4%の精度（つまり熱力学的に整合性のあるデータの相互一致）で明らかになっている。通常1つのデータセットに関して報告される統計的不確かさは（はるかに複雑な分子力場に対しても）上述の値より大幅に小さいことを考慮すると、この現状は満足できるものではない。

相平衡の性質および任意の密度における一様状態の性質はどちらも、一般には分子シミュレーションでしか得ることができないが、ヴィリアル係数は直接レナード-ジョーンズ・ポテンシャルから計算できる。第2および第3ヴィリアル係数の数値データは幅広い温度領域にわたって求められている。これらを図5に示した。さらに高次（16次まで）のヴィリアル係数に関しては、次数が高くなるにつれて得られているデータ点数が減少していく。粘性率、熱伝導と、および自己拡散係数などのレナード-ジョーンズ流体の輸送特性についても研究が続いているが、一様平衡状態の状態方程式や内部エネルギーといった特性に関するデータに比べるとそのデータベースは非常に小さい。

レナード-ジョーンズ固体の性質

流体相に比べて、レナード-ジョーンズ固体に関するデータベースおよび知見は著しく貧弱である。これは、レナード-ジョーンズ・ポテンシャルを固体状態の物質のモデル化に利用することが少ないことが主な理由である。固相、特に金属固相の相互作用を二体加法的相互作用で近似すべきでないことが早くから知られていたからである。

それでも、レナード-ジョーンズ・ポテンシャルは単純で計算効率がいいので固体状態物理で頻繁に利用される。固相および固液相平衡の基礎的性質に関して何度も研究がなされている。

レナード-ジョーンズ物質は、温度および圧力に応じてfcc、hcp およびその他の最密多型格子を形成する（図2参照）。低温で圧力が低い側の領域では、hcpがエネルギー的に有利であるから平衡構造となる。fcc格子は高温かつ高圧でエネルギー的に有利であるから、より広範囲の状態で安定構造となる。fccとhcpの共存線は${\displaystyle T=0}$でおよそ${\displaystyle p=878.5\,\varepsilon \sigma ^{-3}}$から始まり、温度の最大値のおよそ${\displaystyle T=0.4\,\varepsilon k_{\mathrm {B} }^{-1}}$を通って、およそ${\displaystyle T=0.32\,\varepsilon k_{\mathrm {B} }^{-1}}$の気体固体相境界、したがって三重点で終わる。 したがって液相および超臨界相と相平衡になり得る固体はfccのみである（図2参照）。

2つの固相fcc、hcpおよび気相の三重点は

${\displaystyle T_{\mathrm {tr} }=0.32\pm 0.001\,\varepsilon k_{\mathrm {B} }^{-1}}$

${\displaystyle \rho _{\mathrm {tr,gas} }:}$報告なし

${\displaystyle \rho _{\mathrm {tr,fcc} }=1.03859\pm 0.0008\,\sigma ^{-3}}$

${\displaystyle \rho _{\mathrm {tr,hcp} }=1.03861\pm 0.0007\,\sigma ^{-3}}$

${\displaystyle p_{\mathrm {tr} }=0.96\cdot 10^{-9}\,\varepsilon \sigma ^{-3}}$

である。 この値と大きく異なる値を報告している文献もあることに注意しておく。

レナード-ジョーンズ物質の混合系

レナード-ジョーンズ粒子の混合系は主に溶液に関する理論や手法の開発において典型的な系として使われることが多いが、一般の溶液の性質に関する研究にも使われる。その歴史は、ロングエト-ヒギンズ、およびレランドとローリンソンらの共形溶液理論の基礎研究にまでさかのぼる。これらの研究は多くの混合系に関する研究の基礎となっている。

2成分以上のレナード-ジョーンズ混合系は、構成成分のポテンシャル・パラメータ（${\displaystyle \varepsilon }$および${\displaystyle \sigma }$）の少なくとも1つを他の成分のそれと異なる値にすることで設定できる。2成分混合系では、レナード-ジョーンズ・ポテンシャル型の3種類の対相互作用 1-1、2-2、および 1-2 相互作用が生じる（ここで2つの成分を番号1および2で指定した）。異成分相互作用1-2については、パラメータ${\displaystyle \varepsilon _{\mathrm {12} }}$および${\displaystyle \sigma _{\mathrm {12} }}$を${\displaystyle \varepsilon _{\mathrm {11} }}$、${\displaystyle \sigma _{\mathrm {11} }}$、${\displaystyle \varepsilon _{\mathrm {22} }}$および${\displaystyle \sigma _{\mathrm {22} }}$に基づいて決定する方法に関して追加の仮定が必要である。この決定法は組み合わせ規則と呼ばれ、さまざまな（経験的で、厳密な物理的議論に基づいていない）方法がある。 これまでもっともよく使われている組み合わせ規則はローレンツとベルテロによる $${\displaystyle \sigma _{12}=\eta _{12}{\frac {\sigma _{11} \sigma _{22}}{2}}}$$$${\displaystyle \varepsilon _{12}=\xi _{12}{\sqrt {\varepsilon _{11}\varepsilon _{22}}}}$$である。

パラメータ${\displaystyle \xi _{12}}$は状態に依存しない相互作用パラメータである。異成分サイズ・パラメータ${\displaystyle \sigma _{12}}$が算術平均であることが物理的にもっともらしいので、そうなるようにパラメータ${\displaystyle \eta _{12}}$は通常は1に選ぶ。それに対してパラメータ${\displaystyle \xi _{12}}$はモデル混合系の相挙動を再現するように幾何平均を調整するために使う。たとえば状態方程式のような解析的モデルでは通常、幾何平均からの偏差パラメータとして${\displaystyle k_{12}=1-\xi _{12}}$を使う。${\displaystyle \xi _{12}>1}$のとき、異成分間相互作用エネルギーが増え、したがって異種粒子間引力が強くなる。${\displaystyle \xi _{12}<1}$では異種粒子間引力が弱くなる。

レナード-ジョーンズ混合系に関しては、流体および固体相間（つまり気液、液液、気気、固気、固液、および固固）の相平衡が研究できる。したがって、異なるタイプの三重点（三相平衡）および臨界点に加えて、共晶点および共沸点が存在しうる。2成分レナード-ジョーンズ混合系に関して、流体領域（液相および気相さまざまなタイプの平衡）の研究は、固相の相平衡に関する研究に比べてより包括的である。数多くの異なるレナード-ジョーンズ混合系が研究され文献で発表されているが、標準的な系は確立されていない。通常は当座の目的に便利な性質を持つようにレナード-ジョーンズ・パラメータを選ぶことが多いため、結果を比較することが困難であることが多い。

流体相では、${\displaystyle \xi _{12}=1}$の場合に混合系は実質的に（ラウールの法則の意味で）理想的なふるまいを示す。${\displaystyle \xi _{12}>1}$では引力相互作用が優勢で、この混合系は高共沸点となって、気液平衡を安定化するには純粋単成分の蒸気圧に比べて低圧にする必要がある。 ${\displaystyle \xi _{12}<1}$ の場合は斥力相互作用が優勢で混合系は低共沸点を示し、気液平衡を安定化するためには純粋単成分の蒸気圧より高圧が必要である。${\displaystyle \xi _{12}}$の値が特に小さいとき液液溶解度間隙が生じる。固相を含む相平衡のさまざまなタイプについての研究に関する文献もある。また、固相が流体相平衡の間に入り込む場合もある。しかし、固相を含む相平衡に関して発表されている研究の数は少ない。

レナード-ジョーンズ・ポテンシャルの状態方程式

最初のコンピュータ・シミュレーションによってレナード-ジョーンズ・ポテンシャルの特性の評価が可能になって以来、レナード-ジョーンズ・ポテンシャルについて数多くの状態方程式が提案されてきた。状態方程式に関する包括的レビューは文献を参照。

レナード-ジョーンズ流体の状態方程式は、ソフトマター物理および物理化学の分野で非常に重要である。というのは、高分子や会合流体のような複雑流体の状態方程式を開発するときの出発点としてよく使われるからである。

文献では30以上のレナード-ジョーンズ状態方程式が提案されている。これらの状態方程式の包括的評価によると、いくつかの状態方程式は同程度の高い精度を持っているが、特別に優れたものはない。このうち3つの状態方程式は、他の領域では十分に精密であるのに、ある流体領域でたとえば複数のファン・デル・ワールス・ループのような非物理的な挙動を示す。レナード-ジョーンズ流体の大半の熱力学的性質に関して頑健で精密なレナード-ジョーンズ状態方程式はコラファとネズベダの状態方程式だけであることがわかっている。したがって現在ではこの状態方程式が最も有用な選択肢である。さらに、ジョンソンらのレナード-ジョーンズ状態方程式は、実質的に全ての利用可能な参照データに対して、コラファとネズベダの状態方程式に比べて精度が低いことがわかった。 にもかかわらずジョンソンらのレナード-ジョーンズ状態方程式は今でもコラファとネズベダの状態方程式よりずっと頻繁に使われている。

レナード-ジョーンズ・ポテンシャルの長距離相互作用

「真の」あるいは「完全な」レナード-ジョーンズ・ポテンシャル(1)は無限遠まで到達する。分子シミュレーションにおいてレナード-ジョーンズ・ポテンシャルで相互作用する粒子集団の観測可能量を評価する場合、システムサイズが有限であるために、ある有限の距離までしか相互作用を評価できない。このシミュレーションで用いる最大距離をカットオフ半径${\displaystyle r_{\mathrm {c} }}$と呼ぶ。レナード-ジョーンズ・ポテンシャルは球対称であるから、${\displaystyle r_{\mathrm {c} }}$は方向に依存しない定数である。完全なレナード-ジョーンズ・ポテンシャルの（巨視的および微視的な）熱物理学的性質を得るために、カットオフ半径外の寄与を説明する必要がある。

シミュレーションにおける長距離相互作用の影響を考慮し、完全なポテンシャルに対する良い近似を得るためにさまざまな補正法が開発されている。これらの補正法は、流体の構造を単純化する仮定に基づいている。一様流体の平衡状態のように単純な場合には、単純な補正項で優れた結果が得られる。 異なる相が共存する非一様系の場合には、長距離相互作用に関する補正を求めるのは厄介になる。こういった補正は「長距離補正」と呼ばれる。多くの物性の長距離補正について、単純な解析的表式が確立されている。任意の観測量${\displaystyle X}$について、補正されたシミュレーション結果${\displaystyle X_{\mathrm {corr} }}$は、実際にサンプルした値${\displaystyle X_{\mathrm {sampled} }}$および長距離補正値${\displaystyle X_{\mathrm {lrc} }}$から計算できる。たとえばエネルギーについて${\displaystyle U_{\mathrm {corr} }=U_{\mathrm {sampled} } U_{\mathrm {lrc} }}$である。真に無限のカットオフ距離を持つレナード-ジョーンズ・ポテンシャルの観測量に関する仮想的な真の値${\displaystyle X_{\mathrm {true} }}$は、一般には概算することしかできない。

さらに、長距離補正法の質はカットオフ半径に依存する。カットオフ半径が非常に小さい場合、補正法が基づく仮定が通常は成立しない。この例を図7に示した。

レナード-ジョーンズ切断シフテッド・ポテンシャル

レナード-ジョーンズ切断シフテッド（Lennard-Jones truncated and shifted, LJTS）ポテンシャルは完全なレナード-ジョーンズ・ポテンシャルの代わりに利用される。完全なレナード-ジョーンズ・ポテンシャルとLJTSポテンシャルは、異なる熱物理学的性質を持つポテンシャルとして厳密に分けて考えるべきである。LJTSポテンシャルの定義は $${\displaystyle V_{\text{LJTS}}(r)={\begin{cases}V_{\text{LJ}}(r)-V_{\text{LJ}}(r_{\text{end}})&~~~~r\leq r_{\text{end}}\\0&~~~~r>r_{\text{end}},\end{cases}}}$$ ここで $${\displaystyle V_{\text{LJ}}(r)=4\varepsilon \left[\left({\frac {\sigma }{r}}\right)^{12}-\left({\frac {\sigma }{r}}\right)^{6}\right],}$$である。

LJTSポテンシャルは距離${\displaystyle r_{\mathrm {end} }}$で切断し、その位置でのポテンシャルエネルギーの値${\displaystyle V_{\mathrm {LJ} }(r_{\mathrm {end} })}$だけシフトしたポテンシャルである。 シフトする理由は、${\displaystyle r_{\mathrm {end} }}$におけるポテンシャルの不連続な跳びを避けるためである。LJTSポテンシャルに関しては、長距離補正は必要ない。LJTSポテンシャルで最もよく使われるのは${\displaystyle r_{\mathrm {end} }=2.5\,\sigma }$のポテンシャルであるが、別の${\displaystyle r_{\mathrm {end} }}$が使われた文献もある。異なる${\displaystyle r_{\mathrm {end} }}$を持つLJTSポテンシャルは別のポテンシャルであり、その物質もレナード-ジョーンズ物質とは異なると考えなければならない。

LJTSポテンシャルは完全なレナード-ジョーンズ・ポテンシャルよりずっと計算コストがかからず、（臨界点および三重点の存在、非剛体斥力および引力、相平衡などの）物質の本質的物理的性質を保持している。そのため、LJTSポテンシャルは新しいアルゴリズム、シミュレーション法、および理論を試すために利用されることがよくある。

LJTS物質の性質は、使用したシミュレーションのアルゴリズム、つまり分子動力学法あるいはモンテカルロ法の違いによって影響を受けることがある。一般に、このような違いは完全なレナード-ジョーンズ・ポテンシャルの場合には生じない。

${\displaystyle r_{\mathrm {end} }=2.5\,\sigma }$のLJTSポテンシャルの場合、ポテンシャル・エネルギーのシフトはエネルギーの谷の大きさ${\displaystyle -\varepsilon }$のおよそ1/60で、${\displaystyle V_{\mathrm {LJ} }(r_{\mathrm {end} }=2.5\,\sigma )=-0.0163\,\varepsilon }$である。図8は完全なレナード-ジョーンズ・ポテンシャルおよびLJTポテンシャルの気液平衡線の比較である。完全なレナード-ジョーンズ・ポテンシャルはLJTSポテンシャルに比べて著しく高い臨界温度と臨界圧力を示すが、臨界密度の値は非常に近い。 飽和密度に比べて、気化の圧力およびエンタルピーのほうが長距離相互作用から強い影響を受ける。これは切断とシフトが、ポテンシャルを主にエネルギー的に操作しているからである。

レナード-ジョーンズ・ポテンシャルの拡張と変更

分子間ポテンシャルの典型であるレナード-ジョーンズ・ポテンシャルは、多くのもっと精巧で一般化された分子間ポテンシャルの開発の出発点として利用されてきた。レナード-ジョーンズ・ポテンシャルのさまざまな拡張および変更が文献で提案されている。以下に、レナード-ジョーンズ・ポテンシャルに直接関係していて、歴史的に重要かつ現在の研究でも価値あるいくつかのポテンシャルの例を挙げる。他のポテンシャル例は原子間ポテンシャルの記事にある。

• ミー・ポテンシャル このポテンシャルは、レナード-ジョーンズ・ポテンシャルの指数12および6を、パラメータ${\displaystyle \lambda _{\mathrm {rep} }}$および ${\displaystyle \lambda _{\mathrm {attr} }}$として一般化したものである。圧縮率や音速のような熱力学的導関数に基づく物性は分子間ポテンシャルの斥力部分の急峻さに非常に敏感であることが知られており、したがってミー・ポテンシャルを使うことでより精巧にモデル化できる。ミー・ポテンシャルを最初に明示的に定式化したのはエデュアルド・グリュナイゼンである。したがって実際にはミー・ポテンシャルはレナード-ジョーンズ・ポテンシャル以前に提案されている。ミー・ポテンシャルはグスタフ・ミーに因んで名付けられた。
• バッキンガム・ポテンシャル このポテンシャルはリチャード・バッキンガムが提案した。これはレナード-ジョーンズ・ポテンシャルの斥力項を指数関数に置き換え、パラメータを追加したものである。
• ストックマイヤー・ポテンシャル このポテンシャルは W. H. ストックマイヤーに因んで名付けられた。このポテンシャルはレナード-ジョーンズ・ポテンシャルに双極子を重ねたポテンシャルである。したがってストックマイヤー粒子は球対称ではなく方向依存性を持っている。
• 二中心レナード-ジョーンズ・ポテンシャル このポテンシャルは、2つの等価な（つまり同じ${\displaystyle \varepsilon ,\sigma ,m}$を持つ）レナード-ジョーンズ相互作用サイトが剛体ボンドで接続されたものである。しばしば2CLJと呼ばれる。通常、長さ（レナード-ジョーンズ・サイト間距離）をサイズ・パラメータ${\displaystyle \sigma }$より非常に小さくとる。そのため、この分子は2つのレナード-ジョーンズ粒子の大半が融合した形状となる。
• レナード-ジョーンズ切断スプラインド・ポテンシャル このポテンシャルは有用であるがほとんど使われていない。LJTSポテンシャルと同じくある距離${\displaystyle r_{\mathrm {end} }}$で切断されていてそれより長距離の相互作用は持たない。ポテンシャルが切断点で連続になるようにシフトされているLJTSポテンシャルと違い、レナード-ジョーンズ切断スプラインド・ポテンシャルでは連続的に0になるように、望ましい性質を持つスプライン関数を使う。

参考文献

関連項目

• 物性物理学
• 化学